C Program For Arithmetic, Harmonic and Geometric Mean
If n numbers are given this C program calculates the arithmetic mean, harmonic mean and geometric mean of those n numbers using the respective formulae.
Arithmetic mean Formula = sum of all numbers / count of numbers
Example: Arithmetic mean of (10,20,30) = (10+20+30)/3 = 60/3 = 20
The harmonic mean of {a1, a2, a3, a4, . . ., an} is given below
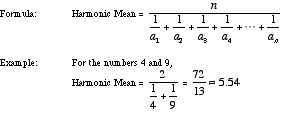
Example: Geometric mean of (7,9,12) = log107 + log109 + log1012 = 2.87852179
Now divide the sum by number of values in the set, in our case 3
Hence Geometric mean (7,9,12) = 2.87852179/3 = 0.959507265
Now take the antilog of the quotient to find out the geometric mean for given set of values (7,9,12)
antilog(0.959507265) =100.959507265 = 9.11
Example: Geometric mean of (3,5,12) = 3x5x12 = 180
Now find the nth root of product where n is the number of values in the given set.
In our case Geometric mean (3,5,12) = ∛(180) ≈ 5.65
It is same as writing (180)1/3>
Calculate Arithmetic Mean
To find arithmetic mean we know thatArithmetic mean Formula = sum of all numbers / count of numbers
Example: Arithmetic mean of (10,20,30) = (10+20+30)/3 = 60/3 = 20
Calculate Harmonic Mean
A harmonic mean is another kind of average. To find the harmonic mean of a set of n numbers, add the reciprocals of the numbers in the set and then divide the sum by n and then take the reciprocal of the result.The harmonic mean of {a1, a2, a3, a4, . . ., an} is given below
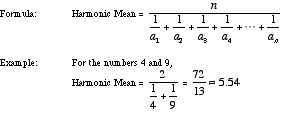
Calculate Geometric Mean
There are two methods to find the geometric mean of n numbers.Find Geometric mean using logarithm
Add the logarithmic values for each number in the set of values given.Example: Geometric mean of (7,9,12) = log107 + log109 + log1012 = 2.87852179
Now divide the sum by number of values in the set, in our case 3
Hence Geometric mean (7,9,12) = 2.87852179/3 = 0.959507265
Now take the antilog of the quotient to find out the geometric mean for given set of values (7,9,12)
antilog(0.959507265) =100.959507265 = 9.11
Geometric Mean Without Using Logarithm
Multiply the values you want to find geometric mean for.Example: Geometric mean of (3,5,12) = 3x5x12 = 180
Now find the nth root of product where n is the number of values in the given set.
In our case Geometric mean (3,5,12) = ∛(180) ≈ 5.65
It is same as writing (180)1/3>
C Program to Find Arithmetic, Harmonic and Geometric Mean of n Numbers
/* Aim:C code to calculate the Arithmetic Mean and Harmonic Mean of two numbers */
#include<stdio.h>
#include<math.h>
int main()
{
int i, op, size;
float sum = 0, Arithmetic_Mean, Harmonic_Mean, Geometric_Mean,numbers[100];
printf("\n How many numbers to accept:- ");
scanf(" %d",&size);
//accept the numbers
for(i=0;i<size;i++)
{
printf("\n Enter %d th number: ",i+1);
scanf(" %f",&numbers[i]);
}
do{
printf("\n\n 1. Arihmetic Mean");
printf("\n 2. Harmonic Mean");
printf("\n 3. Geometric Mean \n");
printf("\n Which operation do you want to perform:- ");
scanf(" %d",&op);
switch(op)
{
case 1:
for(i=0;i<size;i++)
{
sum += numbers[i];
}
Arithmetic_Mean = sum/size;
printf("\n\n The Arithmetic Mean is : %f", Arithmetic_Mean);
break;
case 2:
for(i=0;i<size;i++)
{
sum += (1/numbers[i]);
}
Harmonic_Mean = size/sum;
printf("\n\n The Harmonic Mean is : %f", Harmonic_Mean);
break;
case 3:
sum = 1;
for(i=0;i<size;i++)
{
// we will store the product of all numbers
// in sum varibale
sum *= numbers[i];
}
Geometric_Mean = pow(sum,(float)1/size);
printf("\n\n The Geometric Mean is : %f", Geometric_Mean);
break;
}
}while(op!=4);
return 0;
}Output:
How many numbers to accept:- 3 Enter 1 th number: 10 Enter 2 th number: 20 Enter 3 th number: 30 1. Arihmetic Mean 2. Harmonic Mean 3. Geometric Mean Which operation do you want to perform:- 3 The Geometric Mean (x̄g) is : 18.171207 How many numbers to accept:- 3 Enter 1 th number: 10 Enter 2 th number: 20 Enter 3 th number: 30 1. Arihmetic Mean 2. Harmonic Mean 3. Geometric Mean Which operation do you want to perform:- 3 The Harmonic Mean (H) is : 16.36363636 How many numbers to accept:- 3 Enter 1 th number: 10 Enter 2 th number: 20 Enter 3 th number: 30 1. Arihmetic Mean 2. Harmonic Mean 3. Geometric Mean Which operation do you want to perform:- 3 The Arithmetic Mean (μ) is : 20.00000